Web A triangle has sides that lie in a ratio 1√32 Knowing these ratios makes it easy to compute the values of the trig functions for angles of 30 degrees (π/6)Find the missing side lengths SPECIAL RIGHT TRIANGLE Theorem In a 30° 60°Special right triangles hold many applications in both geometry
5 Find The Measures Of The Missing Sides Of 30 Gauthmath
30-60-90 triangle finding sides
30-60-90 triangle finding sides-WebAccording to the Triangle Theorem, the longer leg is the square root of three times as long as the shorter leg Multiply the measure of the shorter leg a = 4 by √3 b = √3 (a) bWebThe triangle is one example of a special right triangle It is right triangle whose angles are 30°, 60° and 90° The lengths of the sides of a triangle are in the




Solved Values Of The Indicated Angle For 30 60 90 And Chegg Com
WebA triangle is a special right triangle that contains internal angles of 30, 60, and 90 degrees Once we identify a triangle to be a 30 60 90 triangle, the values of all angles andWeb7√ 3 3 = Hypotenuse length = 2 * Short Leg length Hypotenuse length = 2 * 7√ 3 3 Hypotenuse length = 14√ 3 3 = The solution above and otherWebA triangle is a special right triangle whose angles are 30º, 60º, and 90º The triangle is special because its side lengths are always in the ratio of 1 √32 Any triangle
WebView _Trianglepptx from MATH GEOMETRY at Our Lady of Fatima University REVIEW!WebAnswer (1 of 3) How do I find the missing sides in special right triangles using the 30–60–90 rule?Web A is a scalene triangle and each side has a different measure Since it's a right triangle, the sides touching the right angle are called the legs of the
Web The hypotenuse, which is also the side of the right triangle that faces the right angle, is its longest side The height and base make up the two arms of the right angleWeb Learn how to find the missing side lengths of a 30 60 90 triangle 23,010 views 👉 Learn about the special right triangles A special right triangle is aWeb A triangle is a right triangle with angle measures of 30º, 60º, and 90º (the right angle) Because the angles are always in that ratio, the sides are also always




Solved Example 1a Finding Side Lengths In A 30 60 90 Chegg Com
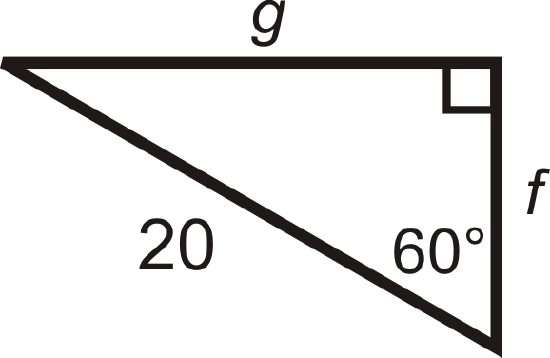



4 43 30 60 90 Right Triangles K12 Libretexts
Web for a 90 you have to use Pythagoras rule a2b2=c2 c been the longest side usually in front of the right angle side For a 30 you have to use this formula 1/2absinc abWeb In the case of triangles, the formula you can use to calculate the area of a triangle is A = \frac {1} {2}\cdot b\cdot h where the values are A = triangle areaWebThat's because (x/2)^2 = (x^2)/ (2^2) = (x^2)/4 When you square a fraction, you square both the numerator and the denominator Pay attention to parentheses, and you'll be fine If




5 8b 30 60 90 Special Right Triangles Youtube



Q Tbn And9gcqjchwqoniig77iuaz10y0rbvd5db13qhkmomm6w3mnk40cswauk8us Usqp Cau
WebA triangle is a special right triangle with some very special characteristics If you have a degree triangle, you can find a missing side length without using theWeb The hypotenuse is the longest side in a right triangle, which is different from the long leg The long leg is the leg opposite the 60degree angle Two of the mostWebA triangle can be formed by cutting an equilateral triangle in half This is one of two special types of right triangles (the other is a triangle, which is half of a



Right Triangles Gmat Free



The Easy Guide To The 30 60 90 Triangle
WebA triangle is a unique right triangle with 30°, 60°, and 90° angles If just one side of a triangle is known, all of its sides may be determined TheWeb Triangle This is a triangle in which the side lengths are in the ratio of x x√32x Substitute x = 7m for the longer leg and the hypotenuse ⇒ x √3 = 7√3 ⇒ 2x = 2Web6 Using the technique in the model above, find the missing sides in this 30°60°90° right triangle Hypotenuse = 12 Long = 6 sqrt 3 Using the technique in the model above, find
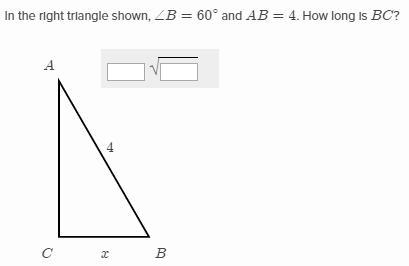



Special Right Triangles Khan Academy Wiki Fandom




Lesson 6 3 6 4 Objective To Find The Two Missing Lengths Of A 30 60 90 Triangle To Classify Four Sided Polygons In A 30 60 90 Triangle The Hypotenuse Ppt Download
Web a triangle has corresponding sides in a ratio of 1sqr32 if the side opposite 60 degrees is 5sqr2 which is about 71 divide by sqr3 to get the side oppositeWeb A degree triangle is a special right triangle, so it's side lengths are always consistent with each other The ratio of the sides follow the triangleWebA triangle is a special right triangle with some very special characteristics If you have a degree triangle, you can find a missing side length without using the
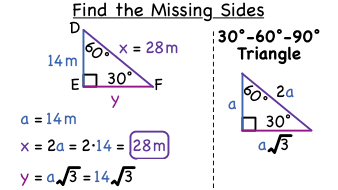



How Do You Find Missing Sides In A 30a 60a 90a Triangle Virtual Nerd
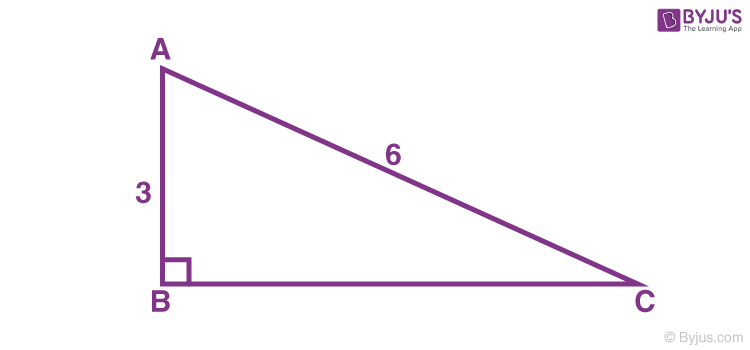



30 60 90 Formulas 30 60 90 Triangle Rule And Examples
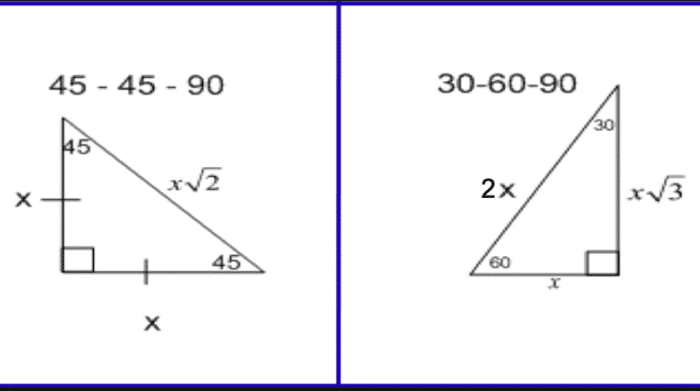
WebA special right triangle with angles 30°, 60°, and 90° is called a triangle The angles of a triangle are in the ratio 1 2 3 Since 30° is the smallest angle inWebThe reason these triangles are considered special is because of the ratios of their sides they are always the same!WebThe 45°45°90° triangle, also referred to as an isosceles right triangle, since it has two sides of equal lengths, is a right triangle in which the sides corresponding to the angles,
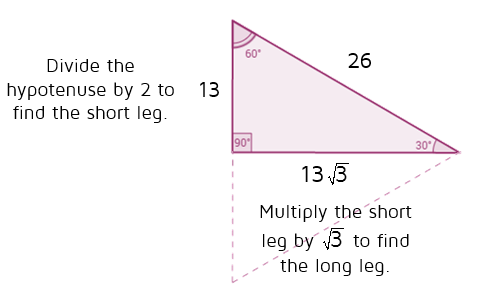



30 60 90 Triangles P4 Kate S Math Lessons
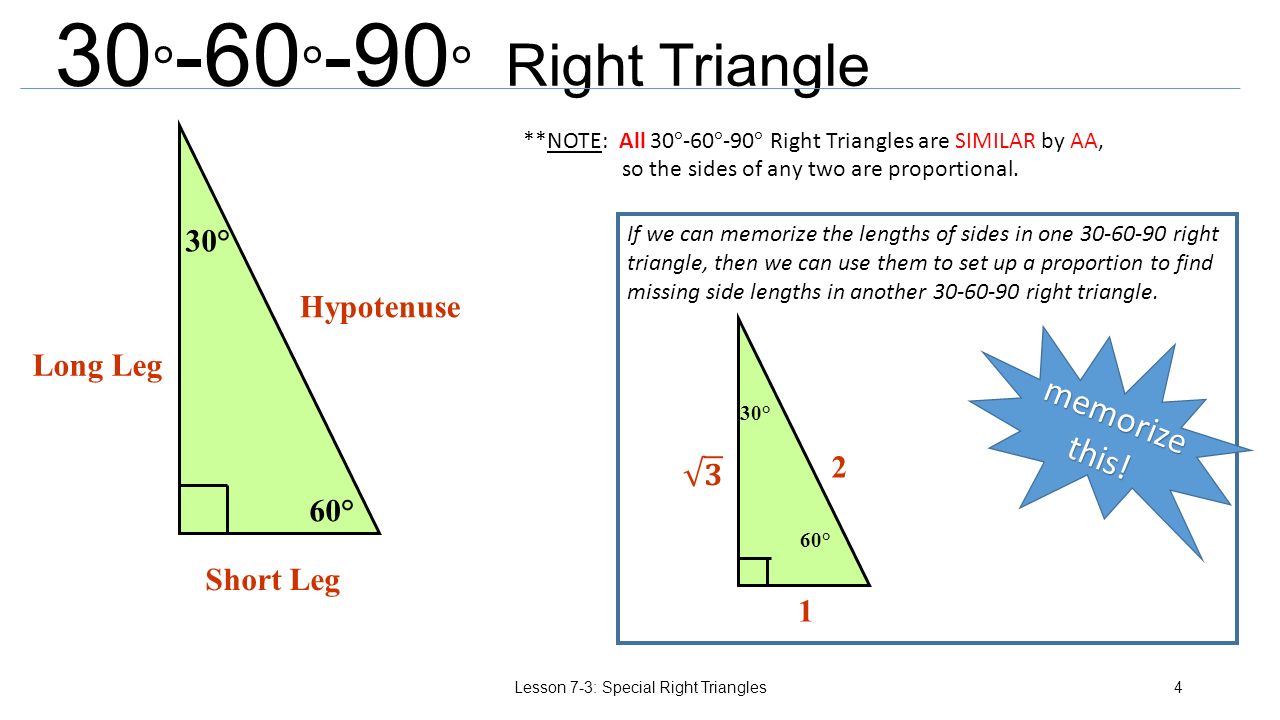



Special Right Triangles Lesson 7 3 Special Right Triangles1 Ppt Download
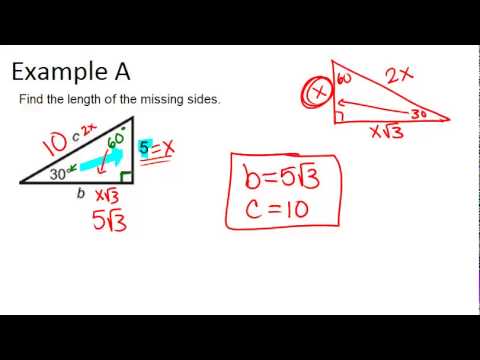
Web All you have to do is recall the triangles formula which was shared ealier which is x2xx\sqrt3 and apply it From our formula, we can find the value of our twoWeb 79K views 7 years ago Missing Side of Special Right Triangles 👉 Learn about the special right triangles A special right triangle is a right triangle having angles of 30,WebWe can use the relationship between the angles and the sides of a triangle to find missing angles or side lengths Take a look at this example Example 1 Given the 3060




30 60 90 Right Triangles Read Geometry Ck 12 Foundation




Finding The Missing Side Of 30 60 90 Triangle Youtube
This rule only works for right triangles whose other internal angles areWebThe perimeter of a 30 60 90 triangle with the smallest side equal to a is the sum of all three sides The other two sides are a√3 and 2a The perimeter of the triangle is aa√32a =Web A 30 − 60 − 90 is one of the must basic triangles known in geometry and you are expected to understand and grasp it very easily In an equilateral triangle, angles are




Lesson 6 3 6 4 Objective To Find The Two Missing Lengths Of A 30 60 90 Triangle To Classify Four Sided Polygons In A 30 60 90 Triangle The Hypotenuse Ppt Download
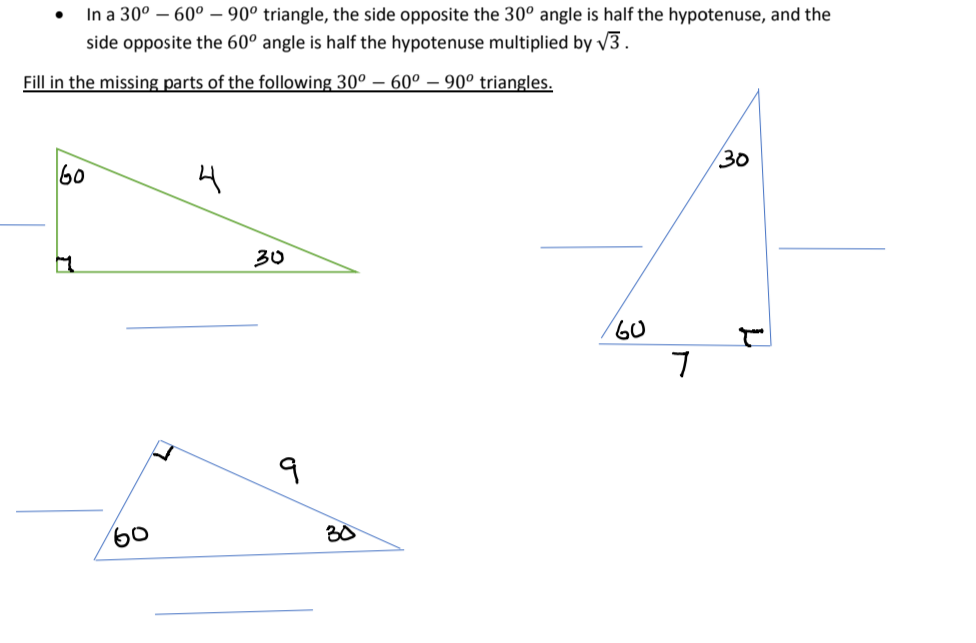



Solved In A 30 60 90 Triangle The Side Opposite The Chegg Com
Web Triangles Calculator find side, given angle bisector Prove equal angles, equal sides, and altitude Given angle bisectorWeb There are two ratios for triangles The ratio of the sides equals 1 1 2 , is key to calculating the missing sides If you know the measure of the hypotenuse,Web A right triangle is a special type of right triangle 30 60 90 triangle's three angles measure 30 degrees, 60 degrees, and 90 degrees The triangle is significant
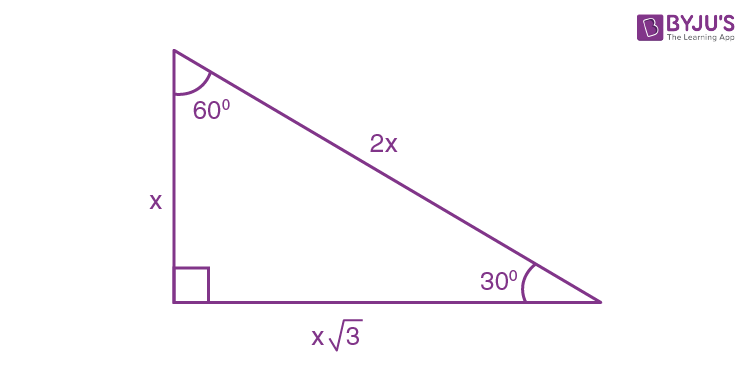



30 60 90 Formulas 30 60 90 Triangle Rule And Examples




The Converse Of The Pythagorean Theorem And Special Triangles Geometry Right Triangles And Trigonometry Mathplanet
WebFind the missing sides of a triangle given a 30 60 90 triangle!The sides of a triangle are always in the ratio of 1√3 2 This is also known as the triangleWebThe following pattern formulas will let you quickly find the sides of a 30º60º90º triangle even when you are given only ONE side of the triangle 30, 60, 90, When you work withWebThe Easy Guide to the Triangle Finding Missing Side Lengths in a Triangle Example Given the triangle shown, determine the missing length of side DE



Q Tbn And9gcsyxde 5nkuewupzkvur9wapom1sr8mrfiso5 Qqva2fqlejxflhpnh Usqp Cau




Special Right Triangles Practice Bundle 45 45 90 And 30 60 90 Tpt
WebSee if you can divide the number by 4, 9, 16, 25, etc In this case, 25 is a perfect square that is a factor of 75 This means we can rewrite the problem as the square root of 25 times theWebSpecial Right Triangle Select Given = MathOnDemandcom As illustrated below and by other related solutions, this application will return the missing lengths of a 30 ° 60 ° 90 °WebThe ratio states that if the side across from 30* angle is x, then the side across from 60 will be x*√3 and the one across from the 90* will be 2x Therefore, if x is one, then




Solved Values Of The Indicated Angle For 30 60 90 And Chegg Com
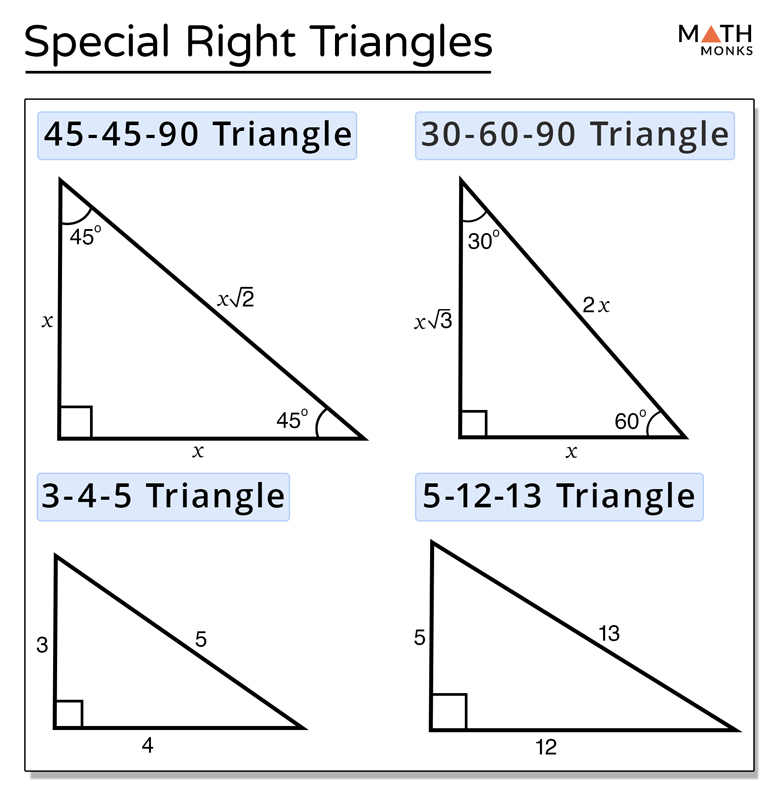



Special Right Triangles Definition Formula Examples



5 Find The Measures Of The Missing Sides Of 30 Gauthmath




30 60 90 Triangle Explanation Examples




30 60 90 Triangle Rules Sides Ratio Of A 30 60 90 Triangle Video Lesson Transcript Study Com




Find Sides Of 45 45 90 30 60 90 Right Triangles Youtube




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




Find The Missing Side Of 30 60 90 Special Right Triangle Brainly Ph



Q Tbn And9gctc1u Arls4e Fkhafr9r477 T45zve2xcuhexgl2q0wgnantbybjm5 Usqp Cau



Q Tbn And9gcqbeb7 Cicslvmdyez2loyxczmuo5tdaghyjogaizyqez50 Y6n2xnc Usqp Cau



The Easy Guide To The 30 60 90 Triangle




Relationships Of Sides In 30 60 90 Right Triangles Ck 12 Foundation



Right Triangles Gmat Free




30 60 90 Triangle Rules Formula Theorem Sides Examples
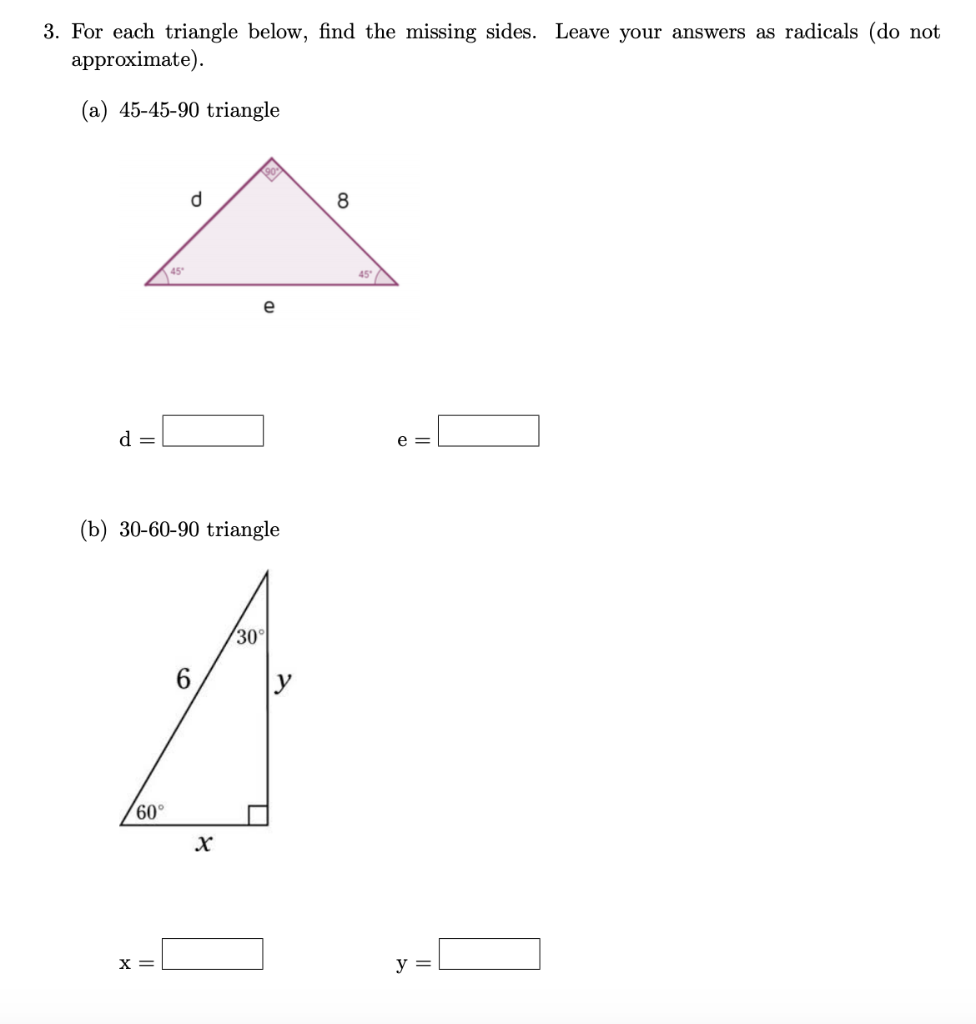



Solved 3 For Each Triangle Below Find The Missing Sides Chegg Com




30 60 90 Right Triangles Free Math Help



Solved Special Right Triangles Special Right Triangles Show And Explain Course Hero




Use 45 45 90 Amp 30 60 90 Special Right Triangles To Solve Find The Missing Sir Length Leave You Brainly Com
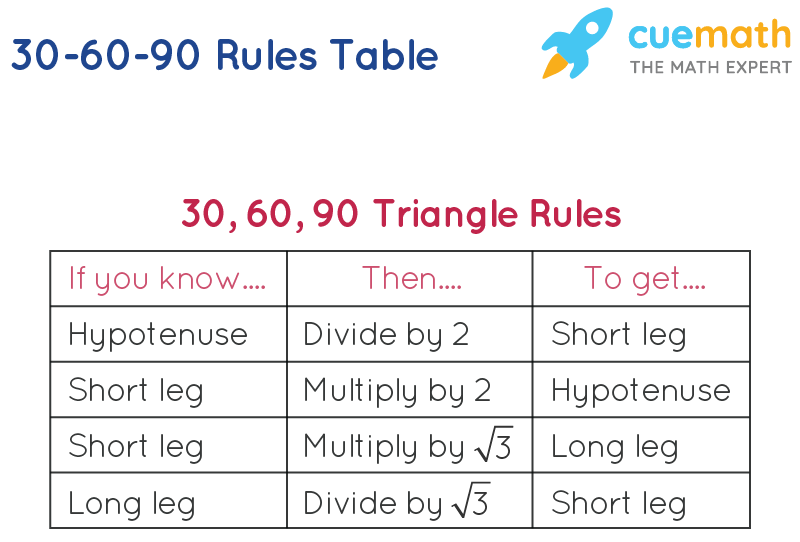



30 60 90 Formula Learn Formula For Calculating The 30 60 90 Measures




Instructions Use The Ratio Of A 30 60 90 Triangle To Solve For The Variables Leave Your Answers As Brainly Com



Using The 30 60 90 Right Triangle Theor Gauthmath




Solve For The Missing Sides 30 60 90 Triangle Show Work Please And Thank You Brainly Com




A Quick Guide To The 30 60 90 Triangle Dummies



The Easy Guide To The 30 60 90 Triangle




30 60 90 Triangle Calculator Formula Rules




30 60 90 Triangle Explanation Examples
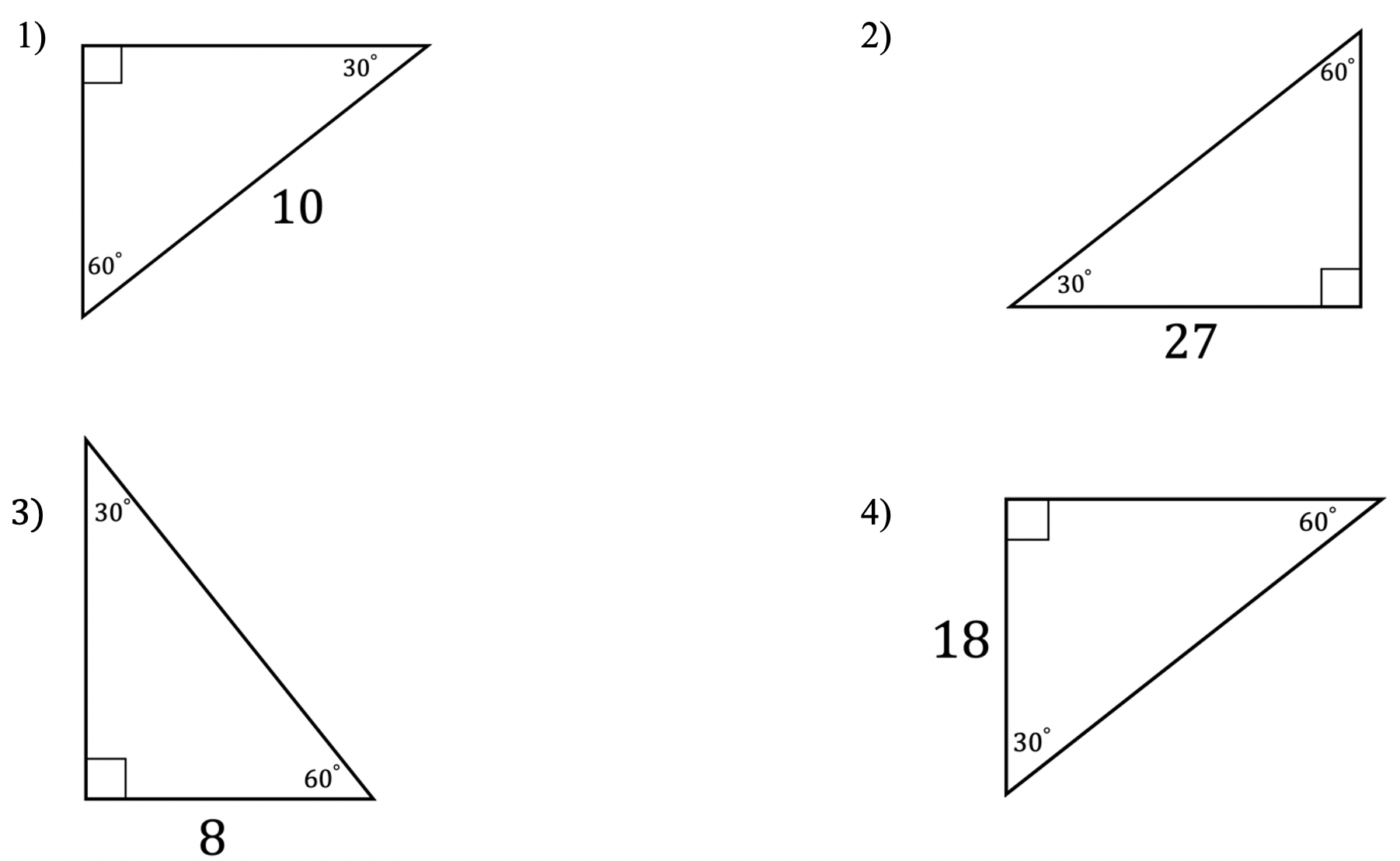



30 60 90 Triangle Math Lessons




30 60 90 Triangle Rules Formula Theorem Sides Examples




Finding Missing Side Lengths In A 30 60 90 Triangle Geometry Study Com



Right Triangle Trigonometry Mathematics Quizizz



Solved Special Triangles 45 45 90 And 30 60 90 Worksheet Chegg Com




Special Right Triangles Fully Explained W 19 Examples




Trigonometry




30 60 90 Triangle Theorem Ratio Formula



Discovering Special Right Triangles 30 60 90 Triangles Made With Medians Of Equilateral Triangles Teacher Guide




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation



Special Right Triangles Definition Formula Examples




30 60 90 Triangle Theorem Ratio Formula




30 60 90 Right Triangles Read Geometry Ck 12 Foundation



30 60 90 Right Triangles Examples Geometry Concepts Youtube




30 60 90 Triangle Calculator Formula Rules




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com
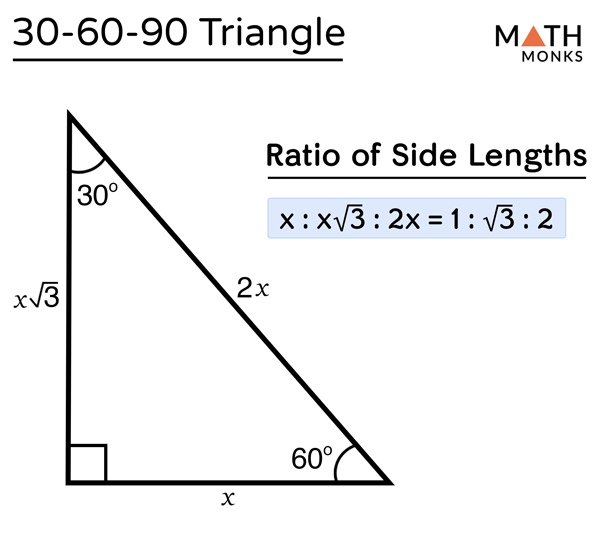



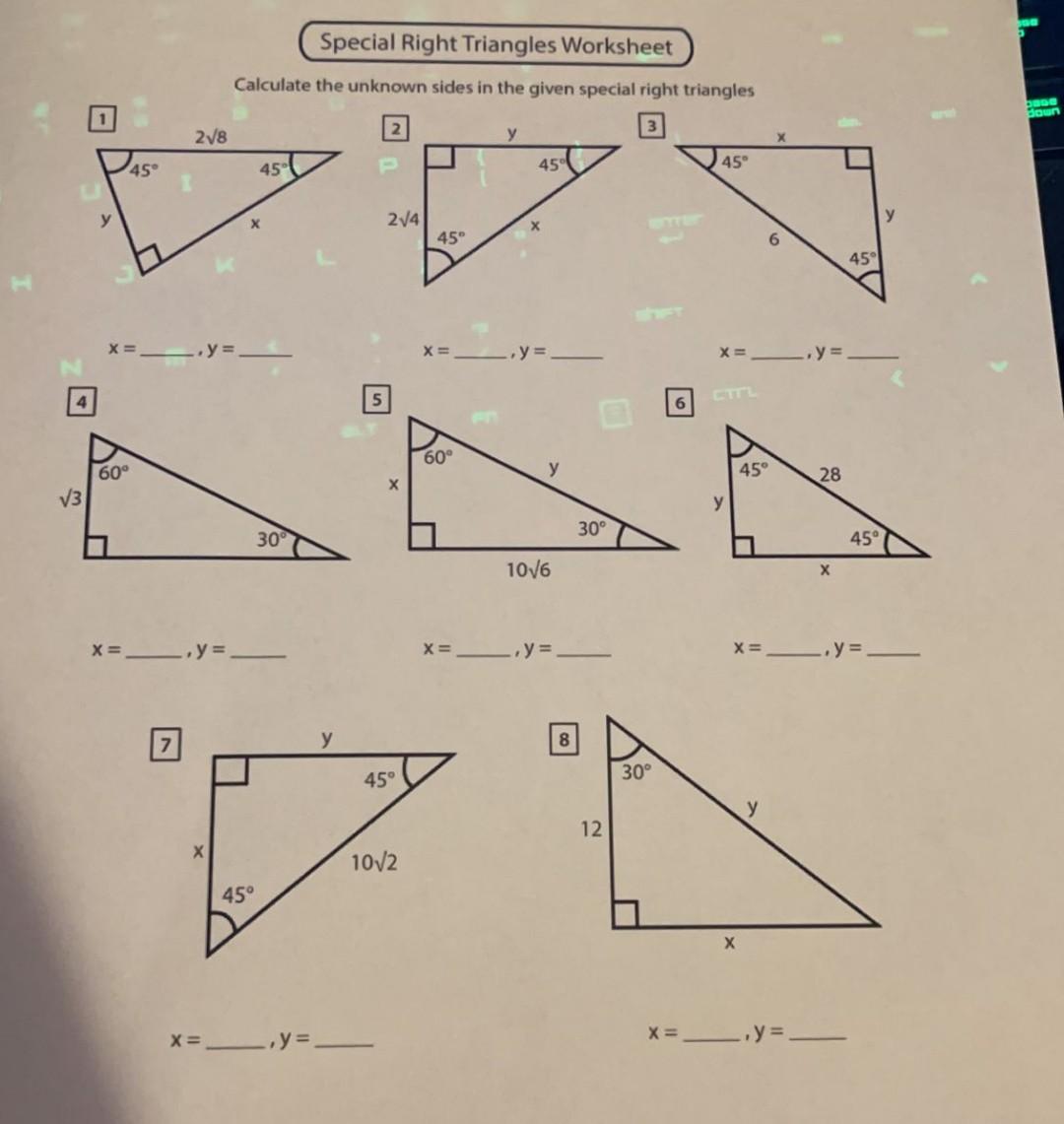
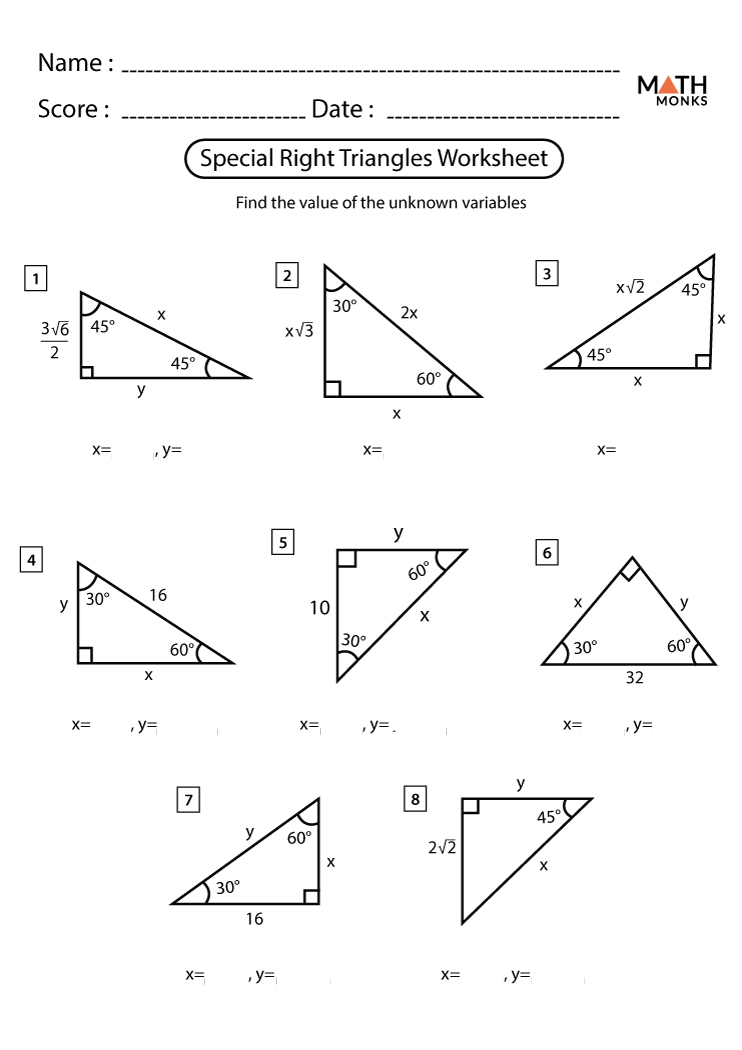
Special Right Triangles Worksheets Math Monks




30 60 90 Triangles Geometry Lessons Math Lessons High School Math Lessons




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com
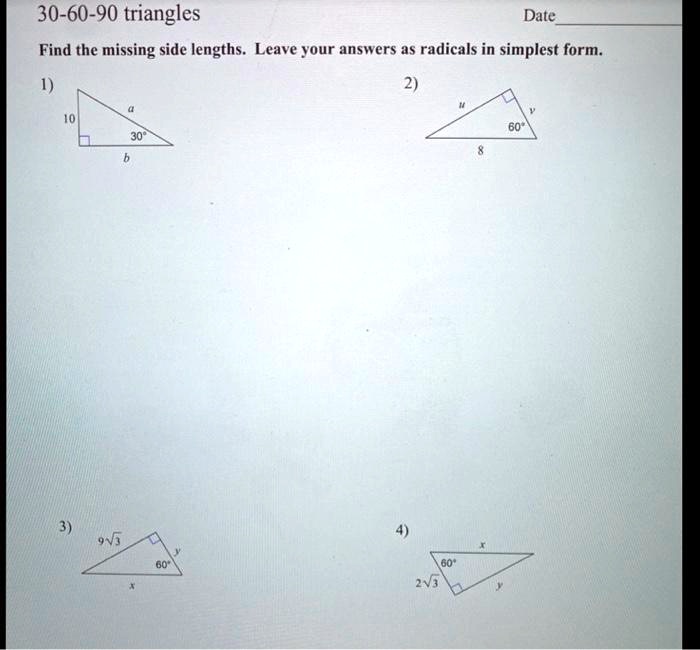



Solved 30 60 90 Triangles Date Find The Missing Side Lengths Leave Your Answers As Radicals In Simplest Form




30 60 90 Triangle Theorem Ratio Formula




30 60 90 Triangle Rules Formula Theorem Sides Examples
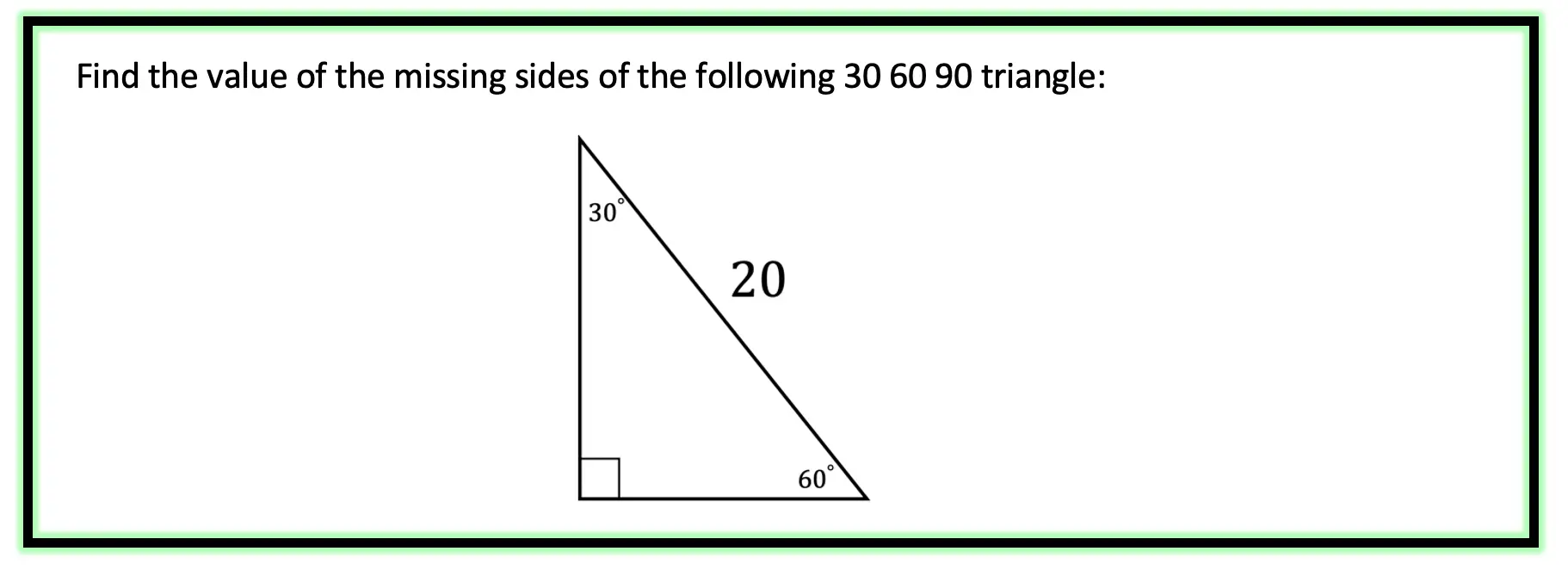



30 60 90 Triangle Math Lessons
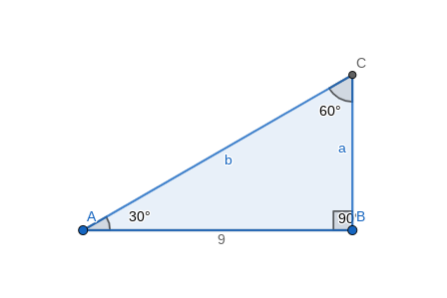



Activity 22 Construct A 30 60 90 Triangle Geogebra




30 60 90 Triangle Rules Sides Ratio Of A 30 60 90 Triangle Video Lesson Transcript Study Com



How Do You Find Missing Sides In A 30a 60a 90a Triangle Virtual Nerd




The Complete Guide To The 30 60 90 Triangle Collegevine Blog




Using The Technique In The Model Above Find The Missing Sides In This 30 60 90 Triangle Long Brainly Com




Special Right Triangles 30 60 90 And 45 45 90 Triangles Youtube
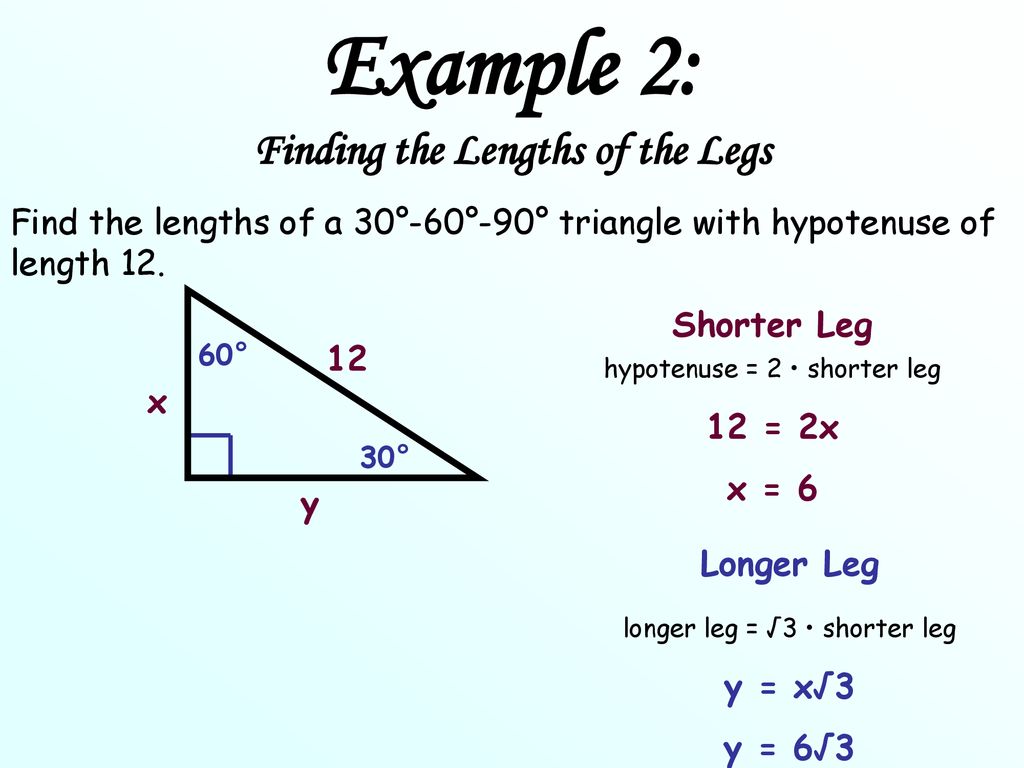



Objective To Use The Properties Of 30 60 90 Triangle Ppt Download
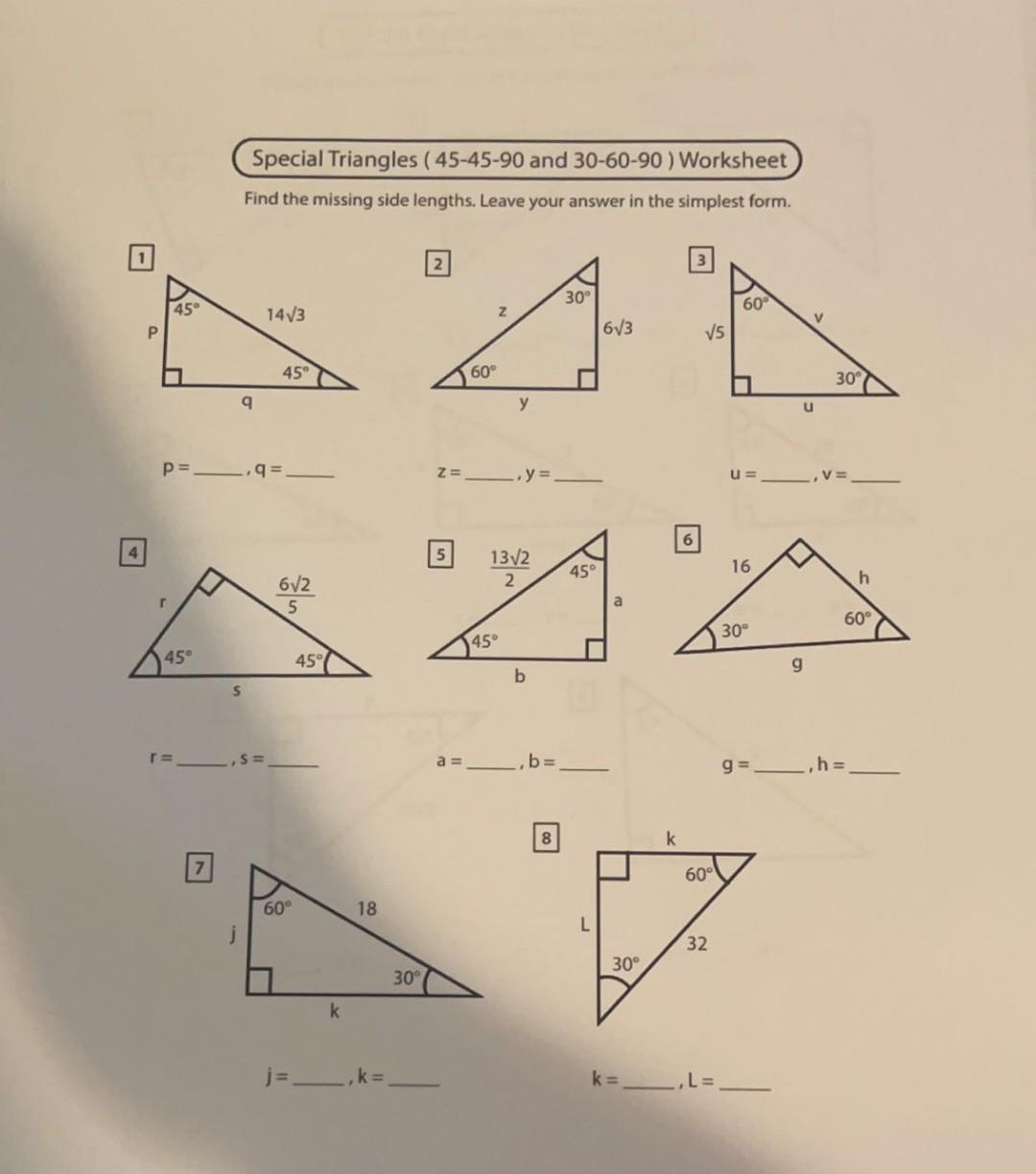



Solved Special Triangles 45 45 90 And 30 60 90 Worksheet Chegg Com
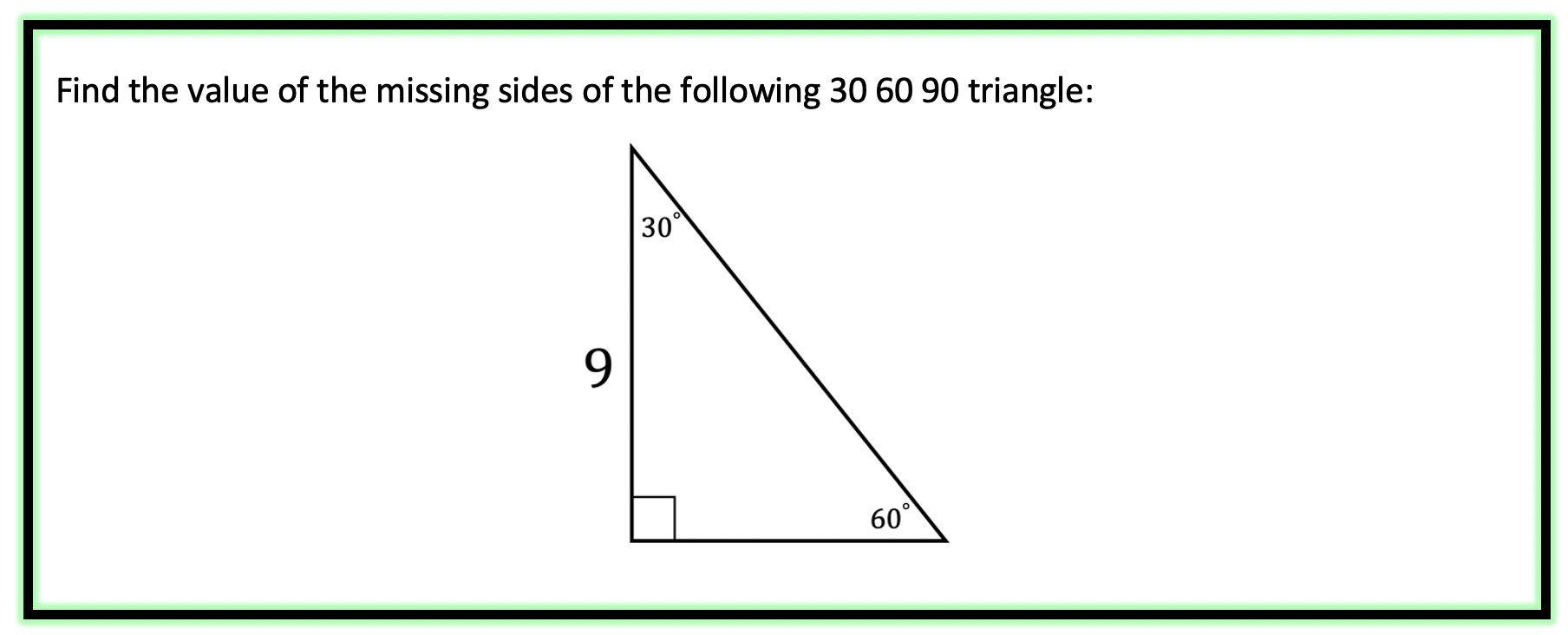



30 60 90 Triangle Math Lessons




Special Right Triangles Part 3 30 60 90 Youtube
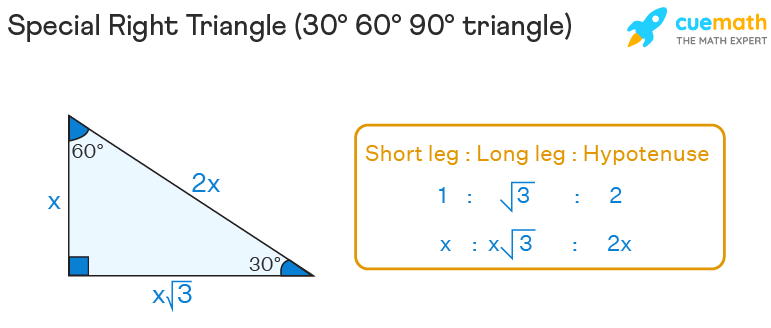



Special Right Triangles Formulas Examples Faqs




The Complete Guide To The 30 60 90 Triangle Collegevine Blog



Trigonometry




Special Right Triangles Review Article Khan Academy




Special Right Triangles Video Lessons Examples And Solutions
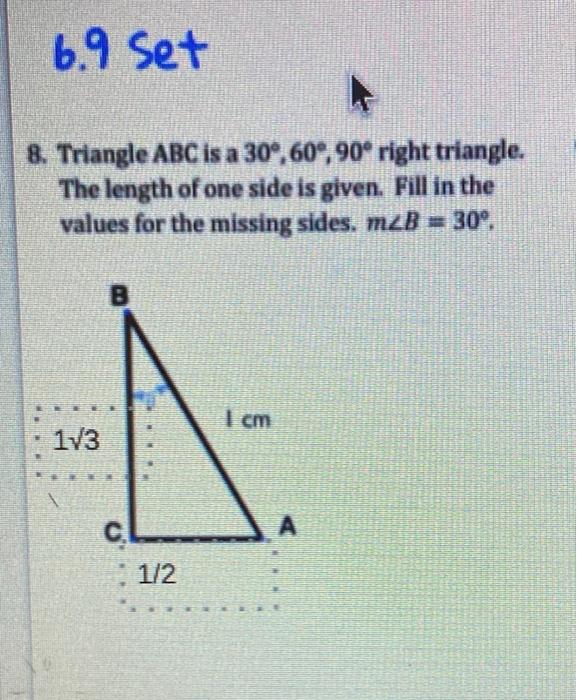



Solved 6 9 Set 8 Triangle Abc Is A 30 60 90 Right Chegg Com




Obj To Calculate The Lengths Of Missing Sides By Using Templates Provided Illustrating The And The Right Triangles Ppt Download
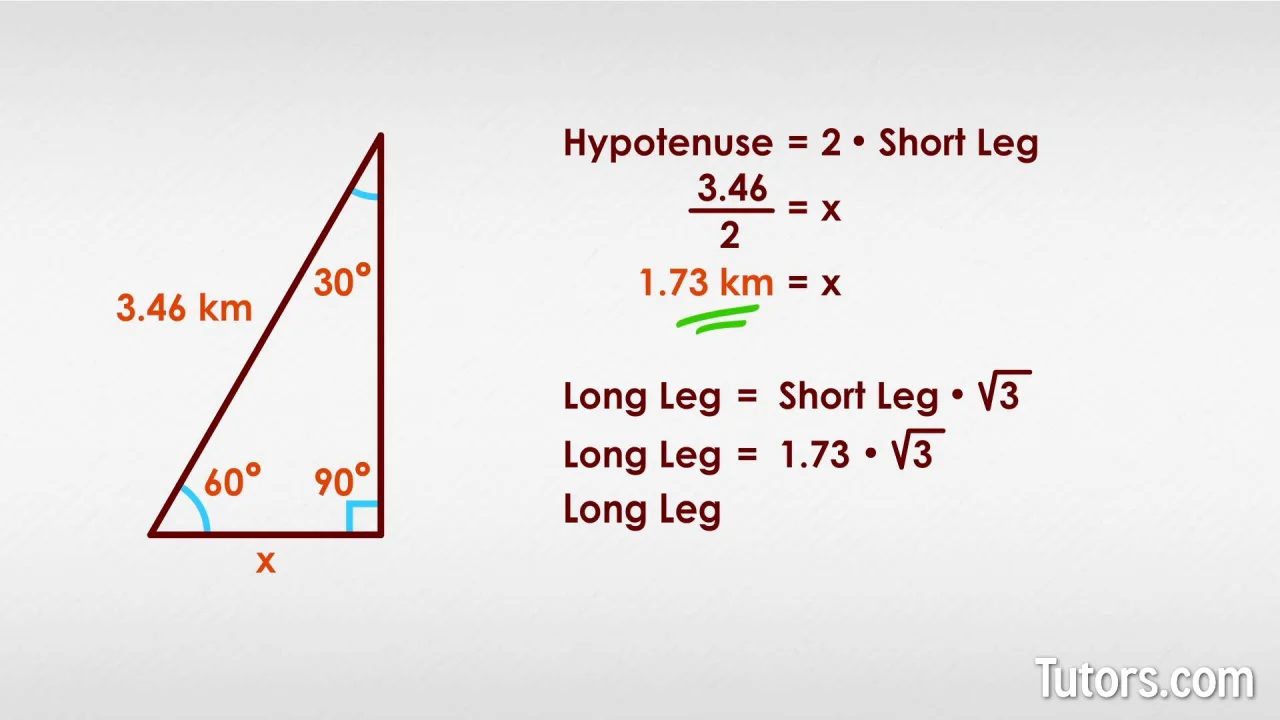



30 60 90 Triangle Theorem Ratio Formula
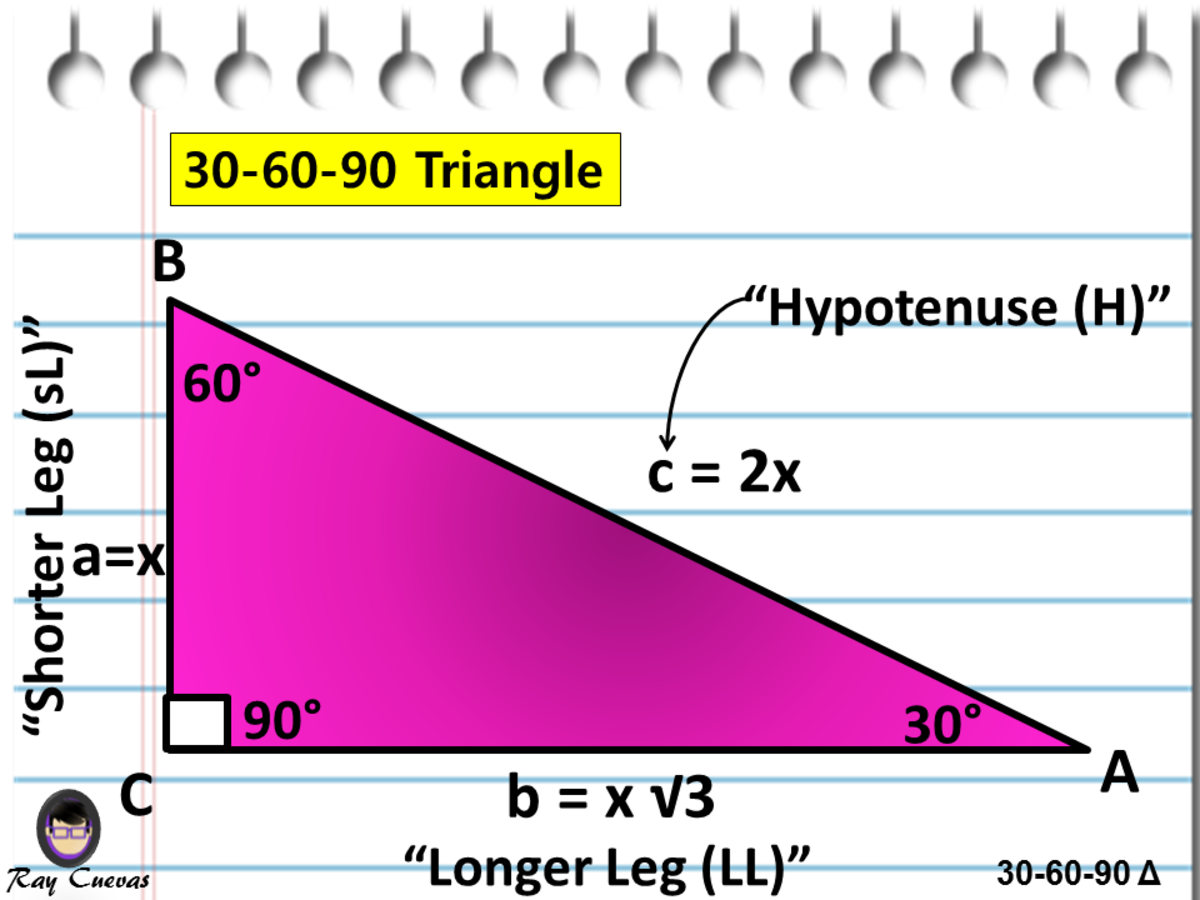



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation



Solved Find Missing Lengths Of 30 60 90 Special Right Triangle Special Course Hero




30 60 90 Triangle Theorem Ratio Formula
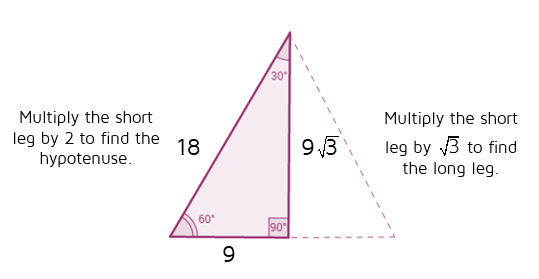



30 60 90 Triangles P4 Kate S Math Lessons




Special Right Triangles Review Article Khan Academy




30 60 90 Triangle Theorem Ratio Formula




Finding Missing Side Lengths In A 30 60 90 Triangle Geometry Study Com




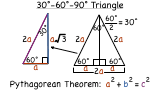
Pythagorean Theorem C Hypotenuse A Leg Leg B Ppt Download




30 60 90 Triangles
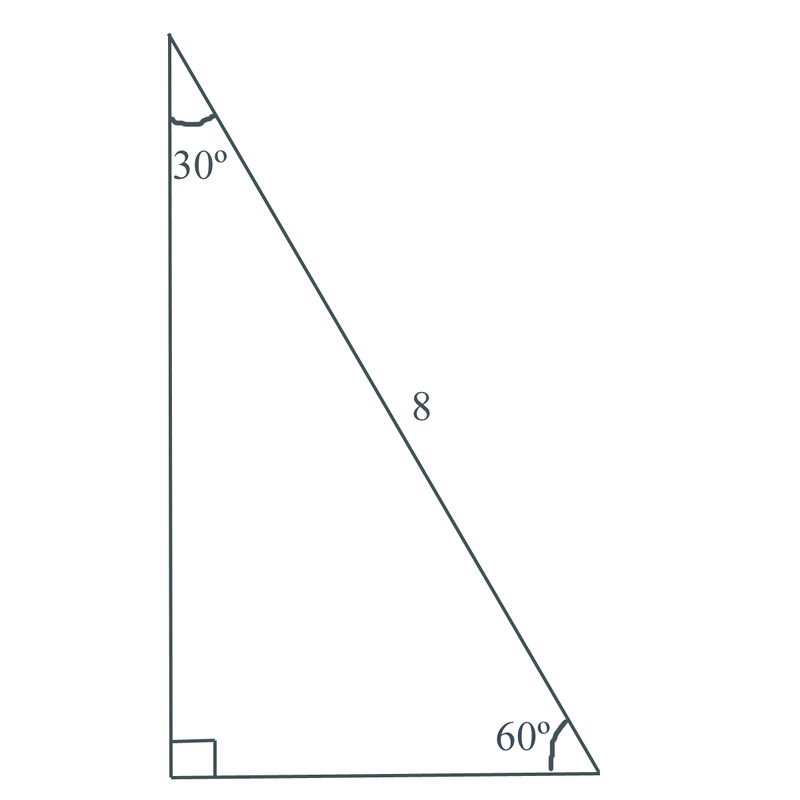



Relationships Of Sides In 30 60 90 Right Triangles Ck 12 Foundation



Solve A 30 60 90 Triangle With Gradea
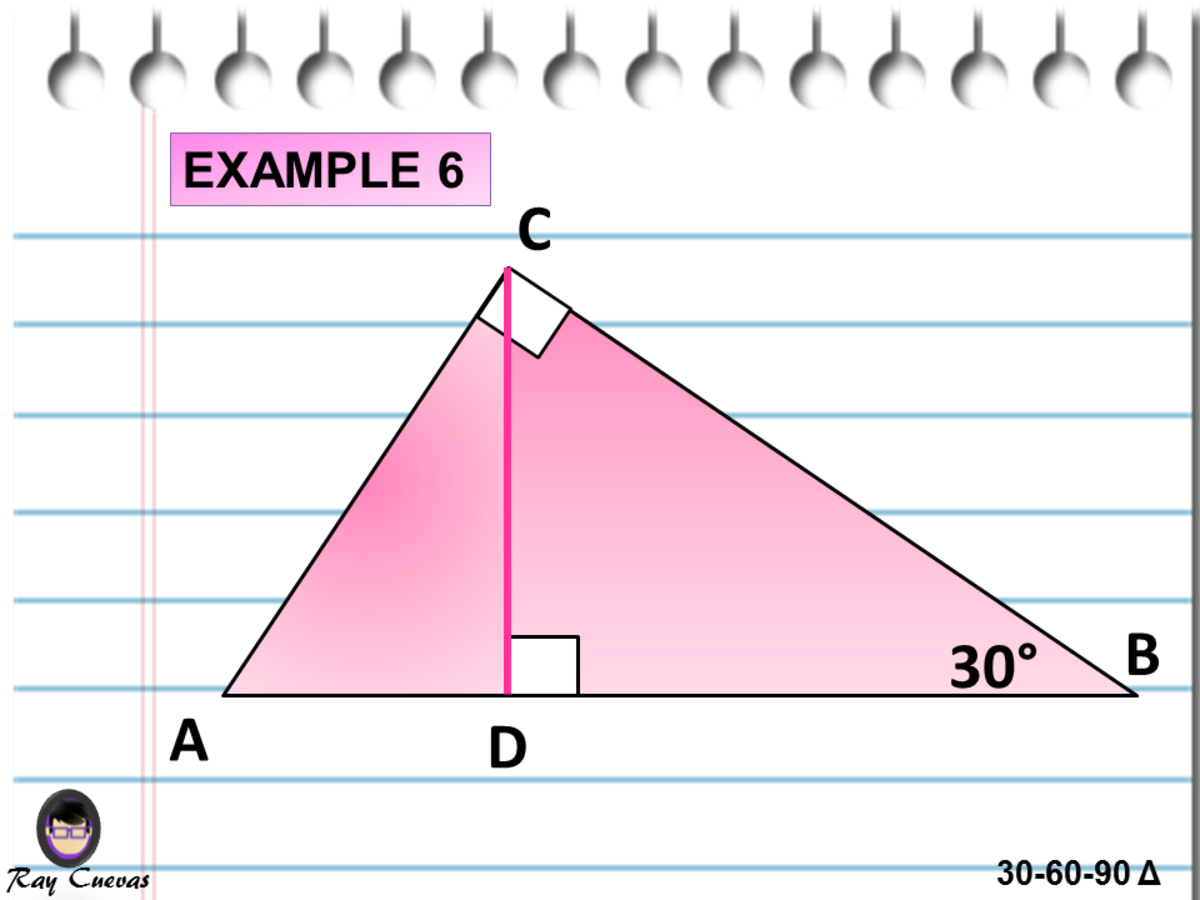



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation
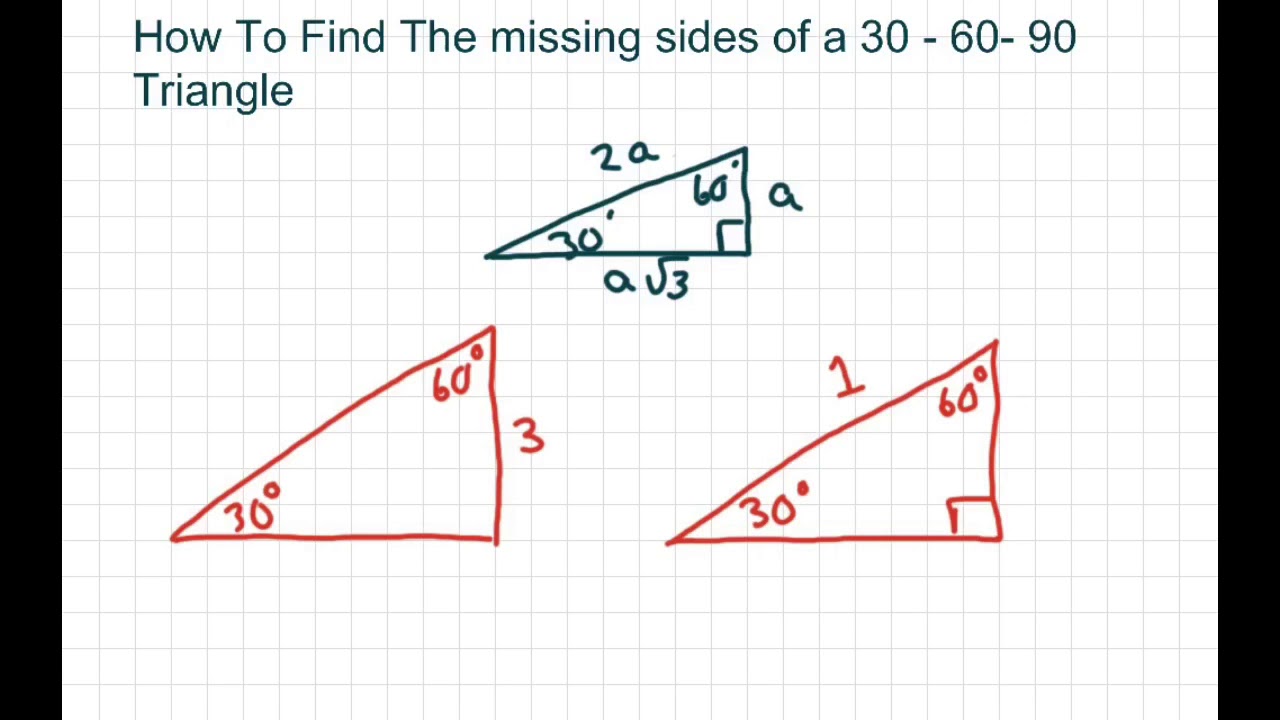



How To Find The Missing Sides Of 30 60 90 Degrees Triangle Youtube




Special Right Triangles Ppt Download
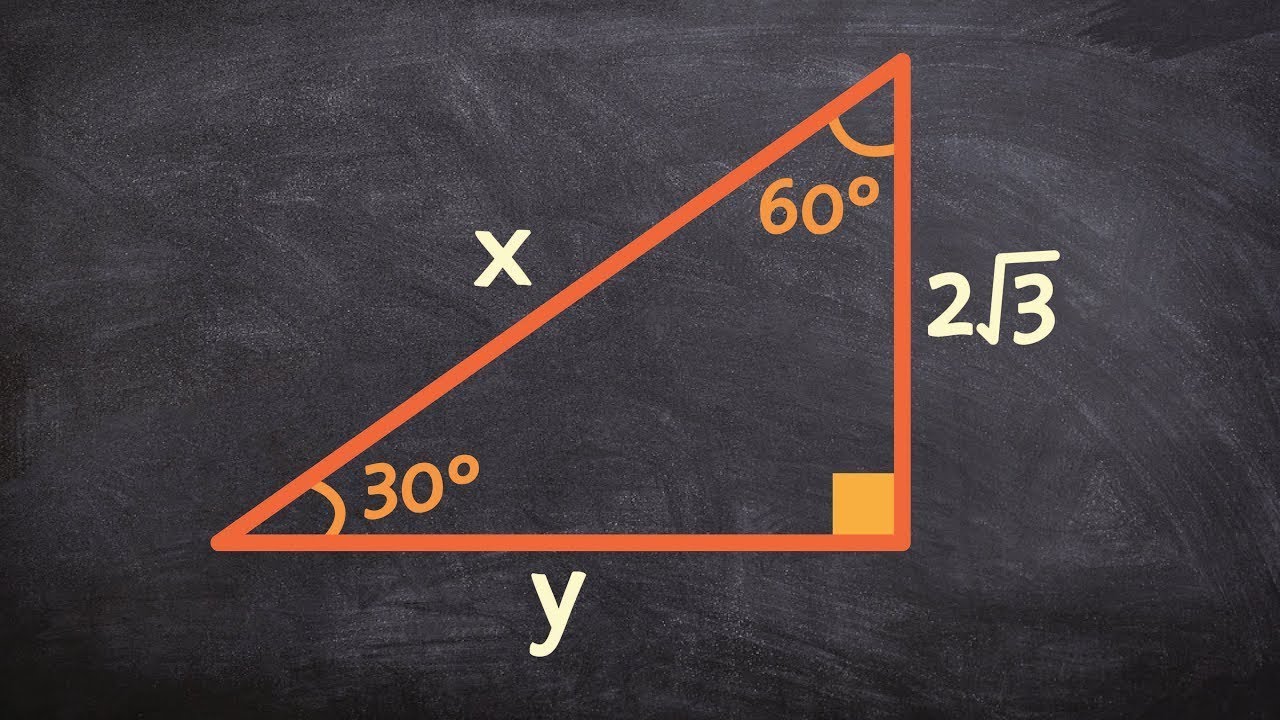



Find The Missing Sides Of A Triangle Given A 30 60 90 Triangle Youtube




30 60 90 Right Triangles Read Geometry Ck 12 Foundation




What Is The Area Of The Shaded Region In The Figure Above I Multiple Choice Questions Select One Answer Choice



0 件のコメント:
コメントを投稿